고정 헤더 영역
상세 컨텐츠
본문 제목
[Coursera1] Neural-Networks-Deep-Learning : Neural Network - Representation, Vectorization, Activation Function, Gradient Descent, Initialization
본문


[ 헷갈렸던 부분에 대한 동기의 답변 ]
로지스틱에서의 가중치 식은 뉴럴 네트워크의 가중치 식중에 가장 쉬운 식이다.
(그래서 NN설명 전에 로지스틱 설명한 거임)
가중치 계산 방법은 비슷한데
1) input 개수
2) activation Function 함수
3) 차수
등에 따라 가중치 그래프 모양이 달라진다.
1 layer NN 을 backward하고,
1 hidden layer(=2 layer NN)NN 도 동일한 방법으로 backward해보자
>> 나중에는 N Layer (Deep Layer)에 대해 Backward할 것이다.


Neural Network 의 하나의 노드들은 다음과 같이 구성되어 있다.
동기가 말한 것처럼 이번 예제에서 z는 다음과 같다.

앞으로 예제에서 사용할 표기법은 다음과 같다.

레이어 내의 노드가 다른 경우 수직으로 쌓는다.
이를 눈으로 확인해보자



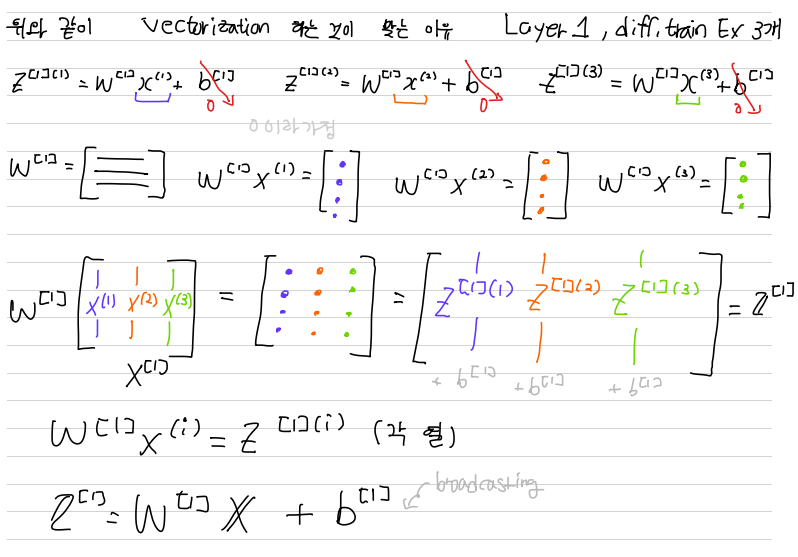
Activation Function의 종류와 선택
activation function 에 sigmoid 말고 다른 것들이 있는가?
: yes!

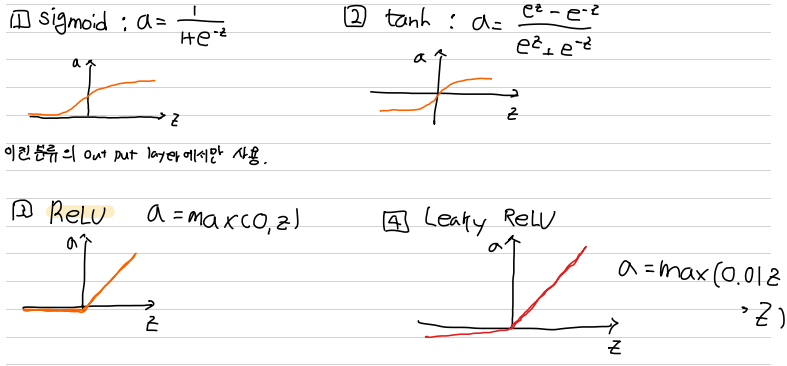

1) (특수경우를 제외하고) sigmoid 보다 tanh를 선택하자
hidden layer에서 activatin Function으로 tanh를 사용하는 것이 좋다.
-1와 1 사이의 값으로 activation 평균은 0에 가깝기에 다음 layer 학습에 효과적이기 때문이다.
! 특수 경우) Output layer의 결과값이 0또는1이 나오는 이진분류 문제이면, 0<=yhat<=1이 효과적이다.
이진 분류 문제 조차도 output Layer에만 sigmoid를 사용하자.
(주의) Sigmoid, tanh 모두 Z가 너무 크거나 작으면, Activation Function의 도함수의 기울기가 매우 작아진다.
이런 경우에, w와 b가 업데이트 되는 속도(=학습 속도)가 매우 느려진다.
2) 왠만한 hidden layer의 Activation Function은 Relu를 사용한다
Relu 함수의 경우 z가 0일 때, 도함수는 정의되지 않지만, z가 0이 될 확률은 낮다 (대부분의 hidden layer에서 z는 양수)
Relu와 Leaky Relu함수는 Sigmoid, tanh와 다르게,
해당 함수의 도함수의 기울기가 많은 Z에 대해 0이 아니다. (학습이 느려질 확률 적음!)
Non- Linear한 Activation Function이 필요한 이유

Gradient descent for Neural Network
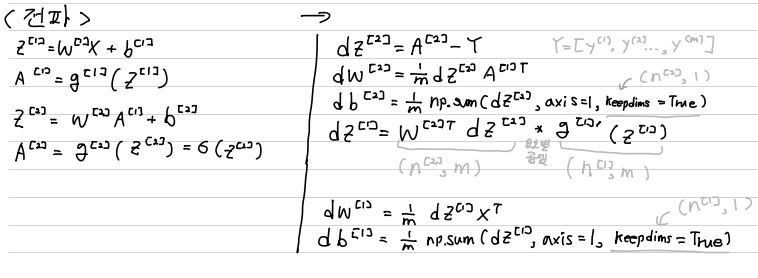
Neural Network에서는 0이 아닌 값으로 Random 하게 initialization해야 한다.
np.random.randn((2,2)) * 0.01



